Angle In A Semicircle

Here we will learn about angles in a semicircle, including their application, proof, and using them to solve more difficult problems.

There are also circle theorem worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

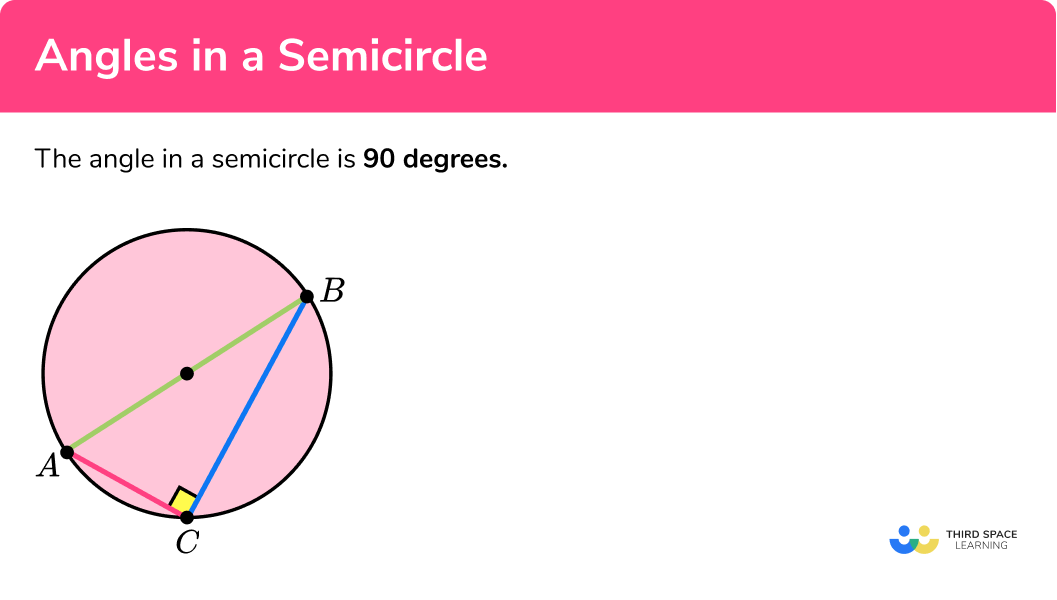
What are angles in a semicircle?

Angles in a semicircle are $90$ degrees:

Angles in a semicircle are created when you join the two ends of the diameter to one point on the arc using chords.

In the diagram above, $AB$ is the diameter of a circle that divides the circle into two. The two points $A$ and $B$ are joined to another point $C$ on the circumference using two chords. This triangle is a right-angle triangle with the $90$ degree angle touching the arc. This is the same for any point that is placed on the arc.

If the point is placed on another point in a semicircle, the result would be the same (the two chords would meet at the circumference at $\pmb{90}$ degrees). The angle in a semicircle is $90$ degrees.

What are angles in a semicircle?

Key parts of a circle needed for this theorem

• The diameter of the circle is the width of a circle, through the centre. The diameter is twice the length of the radius of a circle. In a semicircle, the diameter is the straight edge.
• A chord is a straight line that meets the circumference in two places. The longest chord in a circle is the diameter.
• A semicircle is half of a circle.

Subtended angles (in a semicircle):

An angle within a semicircle is created by two chords meeting at the two ends of the diameter. The diagrams below show the angle subtended by diameter $AC$ from point $B$ for two different semicircles:

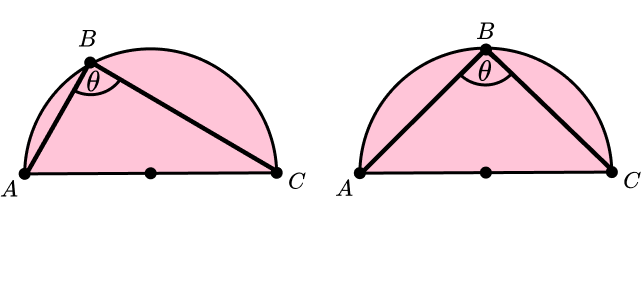
Proving that angles in the same segment are equal

To be able to prove this theorem, you do not need to know any other circle theorem. You just need to be confident with angles in a triangle.

Step	Diagram	Description
1		We start with the diagram of a circle with triangle ABC where A, B, and C are points on the circumference and AB is the diameter of the circle, going through the centre.
2		Connect the centre to the point C to create two smaller triangles.
3		Let us inspect triangle OAC.
4		OA and OC are radii and so triangle OAC is isosceles. This means that the two angles at A and C are equal, so we have labelled them both x.
5		Let us now inspect triangle OBC.
6		OB and OC are radii and so triangle OBC is also isosceles. This means that the two angles at B and C are equal, so we have labelled them both y. We cannot label them both x as they may not be the same as in triangle OAB.
7		So now we have the triangle with the following angles.
8		We can simplify the angle at C (angle ACB) to equal x + y as this angle is the sum of the two angles x and y from the original two triangles OAB and OBC.
9	For the final step in this proof, we need to form and solve an equation to show that x + y = 90°.	As the sum of angles in a triangle is equal to 180°, we can state: As x + y = 90°, we can now state that the angle in a semicircle is 90 degrees.

How to use the angle in a semicircle theorem

In order to use the fact that angles in a semicircle equal $90°$:

1. Locate the key parts of the circle for the theorem.
2. Use other angle facts to determine angles within the triangle.
3. Use the angles in a semicircle theorem to state the other missing angle.

How to use the angle in a semicircle theorem

Related circle theorems

Tangent of a circle is one of 7 circle theorems you will need to know. You may find it helpful to start with our main circle theorems page and then look in detail at the rest.

• Circle theorems
• Angle at the centre
• Angles in the same segment
• Tangent of a circle
• Alternate segment
• Chord of a circle
• Area of a cyclic quadrilateral
• Subtended angles

Angle in a semicircle examples

Example 1: standard diagram

$ABCD$ is an arrowhead where $C$ is the centre of the circle and $A, B,$ and $D$ lie on the circumference. Calculate the size of angle $BAD$:

1. Locate the key parts of the circle for the theorem.

Here we have:

• The angle $ABC = 67°$
• $AB$ is a diameter
• $AC$ and $BC$ are chords
• The angle $CAB = θ$

2Use other angle facts to determine angles within the triangle.

We already know that $ABC=67°$ so we do not need to use any other angle fact to determine this angle for this example.

3Use the angles in a semicircle theorem to state the other missing angle.

As the angle in a semicircle is equal to $90°$, angle $ACB = 90°$. We can therefore use the fact that angles in a triangle total $180°$ to calculate the size of angle $BAC$:

$BAC = 180 - (90 + 67)$

$BAC=23°$

Example 2: cyclic quadrilateral

$ABCD$ is a cyclic quadrilateral. $ACD$ is an isosceles triangle. Calculate the size of angle $ACB$.

Locate the key parts of the circle for the theorem.

Show step

Here we have:

• The angle $BAD = 107°$
• $AC$ is a diameter
• $AB$ and $BC$ are chords
• The angle $ACB = θ$

Use other angle facts to determine angles within the triangle.

Show step

Triangle $ACD$ is interesting because it is an isosceles triangle but also a right angle triangle with the hypotenuse $AC$.

Using the theorem that the angle in a semicircle is $90°$, we can say that angle $ADC$ is equal to $90°$.

As the triangle is isosceles, the other two angles are equal to $(180 - 90) ÷ 2 = 45°$. This is important because we now know that angle $DAC$ is equal to $45°$, and so we can calculate the size of angle $BAC$ which is in the triangle containing θ.

Angle $BAC$ is therefore equal to:

$BAC = 107 - 45$

$BAC = 62°$

We now have the following information added to the diagram:

Example 3: angles in the same segment

Points $A, B, C,$ and $D$ lie on the circumference of the circle. $AD$ is a diameter of the circle. $BD$ and $AC$intersect at the point $E$. Calculate the size of the angle $CDB$.

Locate the key parts of the circle for the theorem.

Show step

Here we have:

• $AD$ is a diameter
• $AB, BD, AC$ and $CD$ are chords
• The angle $BEA = 48°$
• The angle $CAD = 36°$
• The angle $BDC = θ$

Use other angle facts to determine angles within the triangle.

Show step

In order to find the angle θ, we need to know the size of the angle $EDA$. $BED$ is a straight line and so, as angles on a straight line total $180°$, we can calculate angle $AED$:

$AED = 180 - 48$

$AED = 132°$

We can now calculate angle $ADE$ as angles in a triangle total $180°$:

$ADE = 180 - (132 + 36)$

$ADE = 12°$

Example 4: angles in parallel lines

$AC$ and $BD$ are diameters of the circle with centre $O$. $BC$ and $AD$ are parallel. Calculate the size of the angle $OAB$.

Locate the key parts of the circle for the theorem.

Show step

Here we have:

• The angle $COD = 58°$
• $BD$ and $AC$ are diameters
• $OA, OB, OC,$ and $OD$ are radii
• The angle $BAC = θ$

Use other angle facts to determine angles within the triangle.

Show step

$AOD$ is an isosceles triangle as $OA$ and $OD$ are radii. This means that the other two angles are the same and so:

$OAD = (180 - 122) ÷ 2$

$OAD = 29°$

Example 5: the alternate segment theorem

$ABCD$ are points on a circle with centre $O$. $EF$ is a tangent to the circle through the point $C$. $BD$ and $EF$ are parallel. Angle $DCE = 63°$.

Calculate the size of angle $BAC$.

Locate the key parts of the circle for the theorem.

Show step

Here we have:

• The angle $DCE = 63°$
• $AC$ is a diameter
• The angle $BAC = θ$

Use other angle facts to determine angles within the triangle.

Show step

The alternate segment theorem states that angles in the alternate segment are equal. The angle $CBD$ is, therefore, equal to $63°$. Also, as the lines $BD$ and $EF$ are parallel, the line $AC$ is perpendicular to the line $BD$. So the angles at their intersection $G$ are equal to $90°$.

$BCG$ is a triangle. As we know two of the three angles, we can now calculate the size of angle $BCG$, which will help us determine angle $CAB$ as the angles are congruent.

$BCG = 180 - (90 + 63)$

$BCG = 27°$

Example 6: angle at the centre

$A, B, C, D$ and $E$ are points on the circle with centre $O$. Points $A$ and $O$ lie on a line of symmetry. Calculate the size of the angle $DAE$.

Locate the key parts of the circle for the theorem.

Show step

Here we have:

• The angle $DOC = 90°$
• $BE$ is a diameter
• The angle $DAE = θ$

Use other angle facts to determine angles within the triangle.

Show step

The angle at the centre is twice the angle at the circumference and so angle $DAC = 45°$.

As the shape is symmetrical, the angle $OAD$ is half the angle $DAC$. So $OAD = 22.5°$.

Common misconceptions

• Cyclic quadrilateral

The angles that are either end of the diameter total $180°$ as if the triangle were a cyclic quadrilateral. They should total $90°$ as the angle in a semicircle is $90°$.

• Isosceles triangles

The triangle is assumed to be isosceles and so the angles at either end of the diameter are the same.

• A diameter or a chord?

The angle at the circumference is assumed to be $90°$ when the associated chord does not intersect the centre of the circle and so the diagram does not show a semicircle.

• Incorrect angle

The angle that is established as $90°$, is labelled as an angle by the diameter, and not the subtended angle at the circumference.

The next lessons are

• Circles, sectors and arcs
• Equation of a circle
• Circumference of a circle

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.