Cylinder

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

Substitution How to work out perimeter Areas of circles Area of compound shapes Maths formulas Area of quadrilaterals Rounding numbers

This topic is relevant for:

GCSE Maths Geometry and Measure 3D Shapes

Cylinder

Here we will learn about cylinders, including how to find the volume of a cylinder. We will also learn about how to find the curved surface area of a cylinder and its total surface area.

There are also cylinder worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a cylinder?

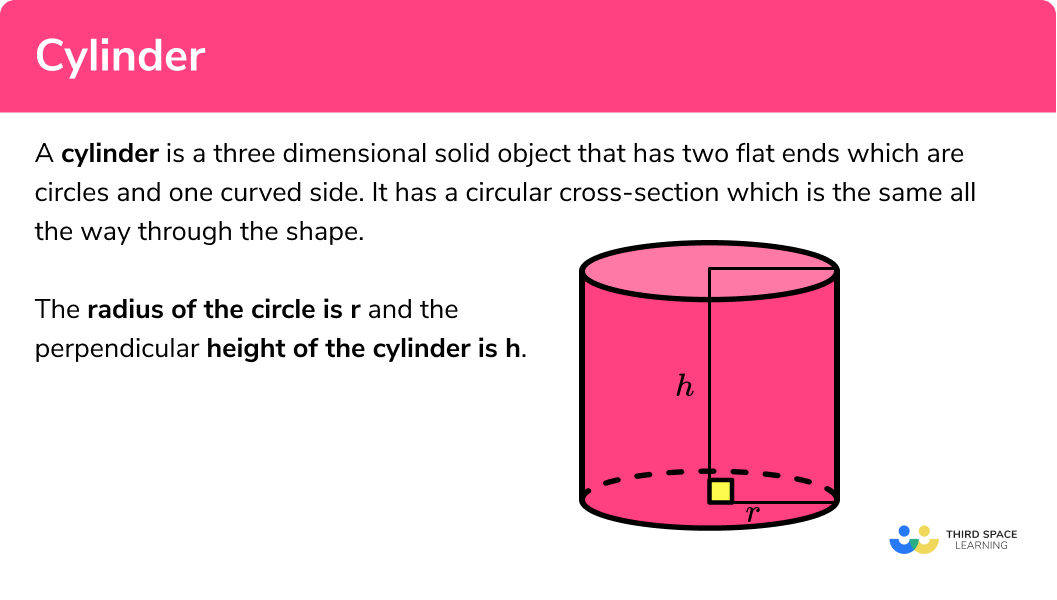
A cylinder is a three dimensional object that has two flat ends which are circles and one curved side. It has a circular cross-section which is the same all the way through the shape.

The radius of the circle is $r$ and the perpendicular height of the cylinder is $h$ .

The cylinders that will feature in GCSE Mathematics are known as right cylinders or right circular cylinders but actually a cylinder can have elliptical ends rather than circular ends. The end shapes just need to be closed curved shapes that lie in parallel planes. It can also have a curved side which is not perpendicular to the base. These are known as oblique cylinders.

What is a cylinder?

Volume of a cylinder

The volume of a cylinder is how much space there is inside a cylinder. t can be found by multiplying the height of a cylinder by the area of its base.

The formula for the volume of a cylinder is:

\text{Volume}=\pi r^2 h

E.g. Find the volume of the cylinder

\begin{aligned} \text{Volume}&=\pi r^2 h\\\\ &=\pi \times 4^2 \times 10\\\\ &=160\pi\\\\ &=502.7 \ cm^3 \ \text{(to 1 dp)} \end{aligned}

Step-by-step guide: Volume of a cylinder

How to calculate the volume of a cylinder

In order to calculate the volume of a cylinder:

Write down the formula.
Substitute the given values.
Work out the calculation.
Write the final answer, including units.

How to calculate the volume of a cylinder

Cylinder worksheet

Get your free cylinder worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Cylinder worksheet

Get your free cylinder worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Volume of a cylinder examples

Example 1: volume of a cylinder

Find the volume of the cylinder with radius $3.8 \; cm$ and perpendicular height $6.1 \; cm.$

Give your answer to $1$ decimal place.

Write down the formula.

\text { Volume } =\pi r^{2} h

2Substitute the given values.

\begin{aligned} \text { Volume } &=\pi r^{2} h \\\\ &=\pi \times 3.8^{2} \times 6.1 \end{aligned}

3Work out the calculation.

\begin{aligned} &=\pi \times 3.8^{2} \times 6.1 \\\\ &=276.724 \ldots \end{aligned}

4Write the final answer, including units.

=276.7 \mathrm{~cm}^{3}(\text { to } 1 . d . p)

Example 2: volume of a cylinder

Find the volume of the cylinder with radius $3 \ cm$ and perpendicular height $7 \ cm.$

Leave your answer in terms of $\pi.$

Write down the formula.

Show step

\text { Volume } =\pi r^{2} h

Substitute the given values.

Show step

\begin{aligned} \text { Volume } &=\pi r^{2} h \\\\ &=\pi \times 6^{2} \times 5 \end{aligned}

Work out the calculation.

Show step

\begin{aligned} &=\pi \times 6^{2} \times 5 \\\\ &=180 \pi \end{aligned}

Write the final answer, including units.

Show step

$=180\pi \; cm^3$ .

Surface area of a cylinder

The surface area of a cylinder is the area which covers the outer surface of a cylinder. The surface area of a cylinder is made up of three parts, a curved surface area and two circular bases.

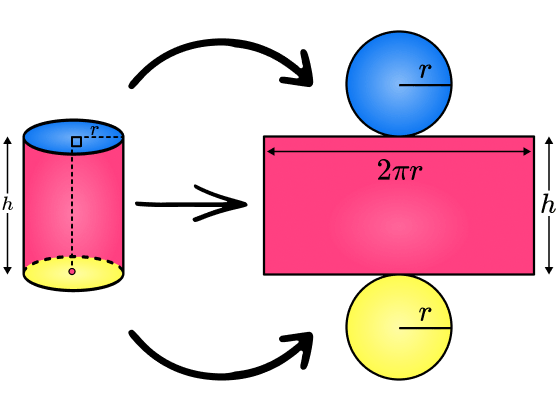
The formula for calculating the curved surface area of a cylinder is:

\text{Curved surface area}=2\pi rh

The formula for calculating the area of a circle:

\text{Area of a circle}=\pi r^2

For the total surface area, we can add the curved surface area to the area of the two circles:

\text{total surface area}=2\pi rh+2\pi r^2

E.g. Find the surface area of cylinder

\text{Curved surface area}=2\pi rh=2\times \pi \times 4 \times 10=80\pi

\text{Area of a circle}=\pi r^2=\pi \times 4^2=16\pi

\begin{aligned} \text{total surface area}&=80\pi +2\times 16\pi \\\\ &=80\pi+32\pi\\\\ &=112\pi\\\\ &=315.9 \ cm^2 \ \text{(to 1 dp)} \end{aligned}

Step-by-step guide: Surface area of a cylinder

How to calculate the surface area of a cylinder

In order to calculate the surface area of a cylinder:

Work out the area of each face.
Add the areas together.
Include units.

How to calculate the surface area of a cylinder

Surface area of a cylinder examples

Example 3: total surface area of a cylinder

Find the total surface area of the cylinder with radius $7.8 \; cm$ and perpendicular height $6.5 \; cm.$

Give your answer to $1$ decimal place.

Work out the area of each face.

Show step

\begin{aligned} \text{Curved surface area}&=2\pi rh\\\\ &=2 \times \pi \times 7.8\times 6.5\\\\ &=318.5574... \end{aligned}

$\begin{aligned} \text{Area of circle }&=\pi r^2\\\\ &=\pi \times 7.8^2\\\\ &=191.1344... \end{aligned}$

Add the areas together.

Show step

Total surface area: $318.5574+191.1344+191.1344=700.8262$

Include units.

Show step

Total surface area $= 700.8 \; cm^2$

Example 4: total surface area of a cylinder

Find the curved surface area of the cylinder with radius $5 \; cm$ and perpendicular height $9 \; cm.$

Leave your answer in terms of $\pi.$

Work out the area of each face.

Show step

\begin{aligned} \text{Curved surface area}&=2\pi rh\\\\ &=2 \times \pi \times 5\times 9\\\\ &=90\pi \end{aligned}

$\begin{aligned} \text{Area of circle }&=\pi r^2\\\\ &=\pi \times 5^2\\\\ &=25 \pi \end{aligned}$

Add the areas together.

Show step

Total surface area: $90 \pi + 25\pi + 25 \pi = 140 \pi$

Include units.

Show step

Total surface area $=140 \pi \; cm^2$

Common misconceptions

Using the correct formula

There are several formulas that can be used, so we need to match the correct formula to the correct context

Rounding

It is important to not round the answer until the end of the calculation. This will mean your final answer is accurate.

Using the radius or the diameter

It is a common error to mix up radius and diameter. Remember the radius is half of the diameter and the diameter is double the radius.

Make sure you have the correct units

For area we use square units such as $cm^2$ .

For volume we use cube units such as $cm^3.$

Did you know…

The name cylinder gets used a lot for objects in real life such as hydraulic cylinders, gas cylinders or hot water cylinders used in heating systems. Not all of these are true cylinders but compound shapes involving hollow cylinders and hemispheres.

Practice cylinder questions

150 \; cm^3

151 \; cm^3

296 \; cm^3

297 \; cm^3

We are finding the volume of a cylinder so we substitute the value of $r$ and $h$ into the formula.

$V=\pi r^2 h$
$V=\pi \times 2.9^2 \times 5.7$
$V=150.598…$
$V=151 \ cm^3 \ \text{(to 3 sf)}$

92\pi \; cm^3

94\pi \; cm^3

90\pi \; cm^3

96\pi \; cm^3

We are finding the volume of a cylinder so we substitute the value of $r$ and $h$ into the formula.

$V=\pi r^2 h$
$V=\pi \times 3^2 \times 10$
$V=90\pi$
$V=90\pi \ cm^3$

430 \; cm^2

428 \; cm^2

429 \; cm^2

427 \; cm^2

We are finding the curved surface area of a cylinder so we substitute the value of $r$ and $h$ into the formula.

Curved surface area $=2\pi rh$
$=2 \times \pi \times 9.5\times 7.2$
$=429.769…$
$=430 \ cm^2 to 3 sf$

42\pi \; cm^3

44\pi \; cm^3

46\pi \; cm^3

48\pi \; cm^3

We are finding the curved surface area of a cylinder so we substitute the value of $r$ and $h$ into the formula.

Curved surface area $=2\pi rh$
$=2 \times \pi \times 4\times 6$
$=48\pi$
$=48\pi \ cm^2$

370 \; cm^2

862 \; cm^2

369 \; cm^2

863 \; cm^2

We are finding the total surface area of a cylinder so we need to find the area of each face and add them together.

Curved surface area $=2\pi rh$
$=2 \times \pi \times 4.2\times 9.8$
$=258.6159…$

Area of circle $=\pi r^2$
$=\pi \times 4.2^2$
$=55.4176…$

144\pi \; cm^3

208\pi \; cm^3

105\pi \; cm^3

130\pi \; cm^3

We are finding the total surface area of a cylinder so we need to find the area of each face and add them together.

Curved surface area $=2\pi rh$
$=2 \times \pi \times 8\times 5$
$=80\pi$

Area of circle $=\pi r^2$
$=\pi \times 8^2$
$=64 \pi$

Total surface area: $80\pi + 64 \pi + 64 \pi = 208\pi$

Cylinder GCSE questions

1. Here is a cylinder.

Cylinder GCSE Question 1

Calculate the volume of the cylinder.

Give your answer to $3$ significant figures.

(2 marks)

Show answer

\pi \times 3.5^2 \times 8.7

(1)

334.815…=335

(1)

2. Here is a cylinder.

Cylinder GCSE Question 2

Calculate the total surface area of the cylinder.

Leave your answer in terms of $\pi$ .

(3 marks)

Show answer

2\times \pi \times 9 \times 6=108\pi

(1)

108\pi + 2\times \pi \times 9^2=108\pi+162\pi

(1)

270\pi

(1)

3. This diagram shows a container.

Cylinder GCSE Question 3

The container is in the shape of a cylinder.

The container is empty.

Tom has a bucket

He is going to use the bucket to fill the container with water.

The bucket holds $12$ litres of water.

How many buckets of water are needed to fill the container?

( $1$ litre $= 1000 \; cm^3$ )

(4 marks)

Show answer

\pi \times 55^2 \times 35

(1)

332 616.12…

(1)

332 616.12… \div 12 000

(1)

$=27.718… = 28$ buckets

(1)

Learning checklist

You have now learned how to:

Calculate the volume of a cylinder

Calculate the curved surface area of a cylinder

Calculate the total surface area of a cylinder

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.